si y solamente si el módulo de v es igual a 1.O en forma más compacta:
Se debe tener en cuenta que con la definición de vector unitario se puede decir que sus coordenadas pueden ser distintas a cero y a uno. Lo único que debes tener en cuenta es que su módulo valga 1.
Ejemplo:
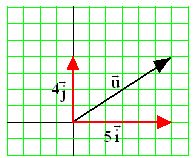
En la figura las coordenadas de
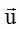
El módulo vale:
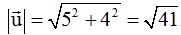
Si divido a las coordenadas (5,4) por
obtendré un nuevo vector cuyas coordenadas serán el cociente de 5 y 4 entre , es decir,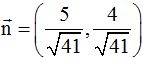 
Comprobamos si el módulo del vector
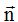vale 1:Efectivamente el vector
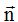es unitario y tiene la misma dirección y sentido que el vector 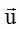.Un vector unitario puede emplearse para definir el sentido positivo de cualquier eje. Así, para los ejes cartesianos x,y,z se emplean los vectores i, j y k.
Los vectores unitarios se utilizan para especificar una dirección determinada y no tienen otro significado físico. Se usan sólo por conveniencia en la descripción de una dirección en el espacio.
No hay comentarios:
Publicar un comentario